Trees seem like an interesting topic but scared to start? Lets start by learning the basics of trees and move on to play with them! Like the trees’ structure in relevance to computer science, we need to start from the root.

What is a Binary Tree?

If you have not read about trees before, this will blow your mind. A recursive definition for trees.

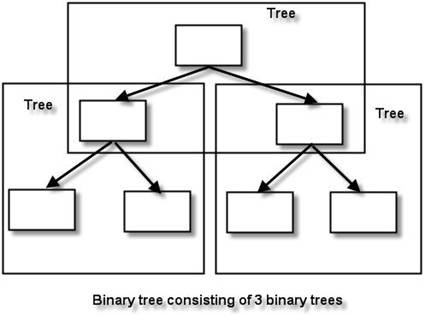
It is either empty, or consists of a root node which has its left and right trees, both of which are binary trees.

Somewhat like this:

Done with the textbook definition, why should we bother about binary trees?

When to choose Trees over linear data structures like Arrays and Linked Lists?

This leads us to:

On what basis we decide which data to use?

• What needs to be stored:Trees are mostly used for storing hierarchical data.
• Cost Of operations:Trees are suitable for operations such as search, insert, delete.

• Memory Consumption:BSTs, if efficiently built use O(lgn) space in average case and O(n) in the worst case.Enough with the introduction, lets go about how to start programming with them.We first of all need to learn how to create a tree. We know about several algorithms given in our textbooks, but we are seldom taught about how to start with them. So let’s start! This is the implementation of a tree node:

struct node{
  int data;
  struct node *left;
  struct node *right;
};

typedef struct node *nodeptr; 

Before calling a create function, we need to data field to label a tree node as well. So we modify the above declaration:

struct node{
  int label; //represents the node number of the tree (0 indexed)
  int data;
  struct node *left;
  struct node *right;
};

typedef struct node *nodeptr; 

Now, we will start creating a tree. We need a function that asks the user to enter the data for a node label. So we have the following prototype: void createTree(nodeptr);

How do we symbolize if a node is leaf?

We initialize its children with data = -1.

In the main function, we need to create a root node:

int main(){
  int data = -1;
  int label = 0;
  printf("Provide data for the root node\n");
  scanf("%d",&data);
  nodeptr root = getnode(label,data);
  createTree(root);
  printf("\n=====================Preorder Traversal====================\n");
  pretrav(root);
  return 0;
}

Now let’s define thecreateTree(nodeptr root) function:

void createTree(nodeptr root){
 if(root == NULL)
 return;
 //Initialize left and right subtrees, which are currently null
 nodeptr left = root->left;
 nodeptr right = root->right;
   //input the left child
  int data = -1;
  printf("Provide data for the left child of node %d (Enter -1 if current node is leaf)\n",root->label);
  scanf("%d",&data);
  if(data != -1){
   left = getnode(2*(root->label)+1,data);
   root->left = left;
  }
  
  //input the right child
  data = -1;
  printf("Provide data for the right child of node %d (Enter -1 if current node is leaf)\n",root->label);
  scanf("%d",&data);
  if(data != -1){
    right = getnode(2*(root->label)+2,data);
    root->right = right;
  }
  createTree(left);
  createTree(right);
 }

Like we see in the main function above, we first use the getnode() function to get the root node, ask the user to enter the data for root node, call the createTree() function, and then ask data for subsequent nodes.

As you can see, this is a recursive function, after taking the data for left and right nodes, you recur over the left and right subtrees.

As you can see, the left and right child of the root node are only initialized with data if data!= null, hence if the noed is leaf, we enter data as -1.

You can find the code above here in C and here, here in java.